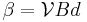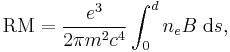Faraday effect

In physics, the Faraday effect or Faraday rotation is a magneto-optical phenomenon, or an interaction between light and magnetic field in a medium. The rotation of the plane of polarization is proportional to the intensity of the component of the applied magnetic field in the direction of the beam of light.

The Faraday effect, discovered by Michael Faraday in 1845, was the first experimental evidence that light and electromagnetism are related. The theoretical basis for that relation, now called electromagnetic radiation, was further developed by James Clerk Maxwell in the 1860s and 1870s. This effect occurs in most optically transparent dielectric materials (including liquids) when they are subject to strong magnetic fields.

The Faraday effect is a result of ferromagnetic resonance when the permittivity of a material is represented by a tensor. This resonance causes waves to be decomposed into two circularly polarized rays which propagate at different speeds, a property known as circular birefringence. The rays can be considered to re-combine upon emergence from the medium, however owing to the difference in propagation speed they do so with a net phase offset, resulting in a rotation of the angle of linear polarization.

There are a few applications of Faraday rotation in measuring instruments. For instance, the Faraday effect has been used to measure optical rotatory power, for amplitude modulation of light, and for remote sensing of magnetic fields. The Faraday effect is used in spintronics research to study the polarization of electron spins in semiconductors.

Faraday rotators are used in laser regenerative amplifier setups.

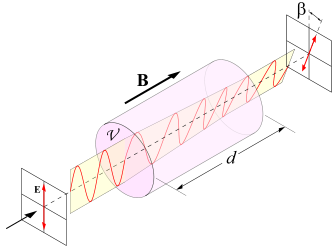
The relation between the angle of rotation of the polarization and the magnetic field in a diamagnetic material is:

Polarization rotation due to the Faraday effect
\beta = \mathcal{V}Bd

where

β is the angle of rotation (in radians)
B is the magnetic flux density in the direction of propagation (in teslas)
d is the length of the path (in meters) where the light and magnetic field interact
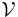\mathcal{V} is the Verdet constant for the material. This empirical proportionality constant (in units of radians per tesla per meter) varies with wavelength and temperature and is tabulated for various materials.

A positive Verdet constant corresponds to L-rotation (anticlockwise) when the direction of propagation is parallel to the magnetic field and to R-rotation (clockwise) when the direction of propagation is anti-parallel. Thus, if a ray of light is passed through a material and reflected back through it, the rotation doubles.

Some materials, such as terbium gallium garnet (TGG) have extremely high Verdet constants (≈ −40 rad T–1 m–1). By placing a rod of this material in a strong magnetic field, Faraday rotation angles of over 0.78 rad (45°) can be achieved. This allows the construction of Faraday rotators, which are the principal component of Faraday isolators, devices which transmit light in only one direction.

Similar isolators are constructed for microwave systems by using ferrite rods in a waveguide with a surrounding magnetic field.

Contents

Faraday rotation in the interstellar medium

The effect is imposed on light over the course of its propagation from its origin to the Earth, through the interstellar medium. Here, the effect is caused by free electrons and can be characterized as a difference in the refractive index seen by the two circularly polarized propagation modes. Hence, in contrast to the Faraday effect in solids or liquids, interstellar Faraday rotation has a simple dependence on the wavelength of light (λ), namely:

\beta = \mathrm{RM} \lambda^2 \,

where the overall strength of the effect is characterized by RM, the rotation measure. This in turn depends on B, and the number density of electrons, ne, both of which may vary along the propagation path, to give (in cgs units):

\mathrm{RM} = \frac{e^3}{2\pi m^2c^4}\int_0^d n_e B \;\mathrm{d}s,

where

e is the charge of an electron;
m is the mass of an electron;
c is the speed of light in a vacuum.

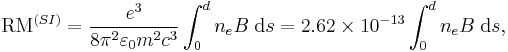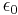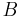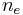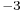(In SI units, \mathrm{RM}^{(SI)} = \frac{e^3}{8\pi^2 \varepsilon_0 m^2c^3}\int_0^d n_e B \;\mathrm{d}s = 2.62 \times 10^{-13} \int_0^d n_e B \;\mathrm{d}s, where \epsilon_0 is the vacuum permittivity; with B in teslas (T), and n_e in m^{-3} (electrons per cubic meter), 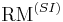\mathrm{RM}^{(SI)} is in radians per square meter (rad/m²).)

Faraday rotation is an important tool in astronomy for the measurement of magnetic fields, which can be estimated from rotation measures given a knowledge of the electron number density[1]. In the case of radio pulsars, the dispersion caused by these electrons results in a time delay between pulses received at different wavelengths, which can be measured in terms of the electron column density, or dispersion measure. A measurement of both the dispersion measure and the rotation measure therefore yields the weighted mean of the magnetic field along the line of sight. The same information can be obtained from objects other than pulsars, if the dispersion measure can be estimated based on reasonable guesses about the propagation path length and typical electron densities. In particular, Faraday rotation measurements of polarized radio signals from extragalactic radio sources occulted by the solar corona can be used to estimate both the electron density distribution and the direction and strength of the magnetic field in the coronal plasma[2]

Faraday rotation in the ionosphere

Radio waves passing through the Earth's ionosphere are also subject to Faraday rotation; as the above equation indicates, the effect is proportional to the square of the wavelength. At a UHF frequency of 435 MHz, where the wavelength is around 70cm, one should expect in the order of 1.5 complete rotations of the polarization as it transits the ionosphere, whereas for 1.2GHz microwave radiation with a wavelength around 25cm, less than a quarter of one rotation is likely. One consequence is that although most radio transmitting antennas are either vertically or horizonally linear polarized, it is difficult to predict what the polarization of the waves from these antennas will be when they arrive at a receiver after reflection in the ionosphere.

See also

External links

References

  1. ↑ Longair, Malcolm (1992). High Energy Astrophysics. Cambridge University Press. ISBN 0521435846. 
  2. ↑ Mancuso S. and Spangler S. R. "Faraday Rotation and Models for the Plasma Structure of the Solar Corona" (2000), The Astrophysical Journal, 539, 480–491